Basins of Attraction - Grundlagen und Algorithmen
Wendet man für eine Funktion f : D → ℂ mit D ⊆ ℂ zur Lösung der Gleichung f (z) = 0 ein Iterations-verfahren an, so nennt man die Folge { zi } mit dem Startpunkt z0 ϵ B ⊆ ℂ, die gegen die Nullstelle ζ konvergiert, einen Orbit von z0; ζ ist ein Attraktor für z0. Die Menge aller Startpunkte z0 ϵ B, die gegen ζ konvergieren, ist der Einzugsbereich (Basin of Attraction) von ζ.
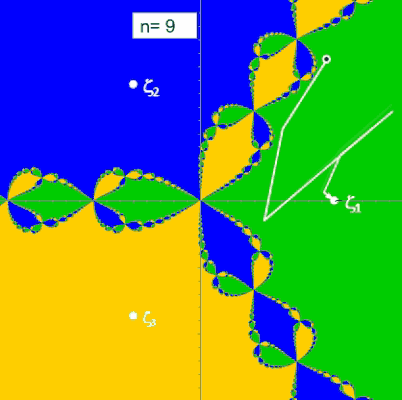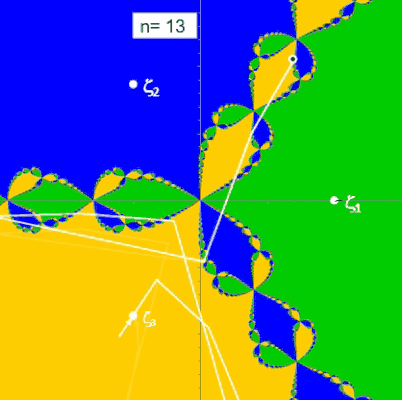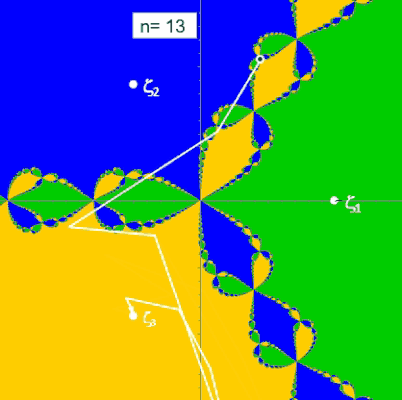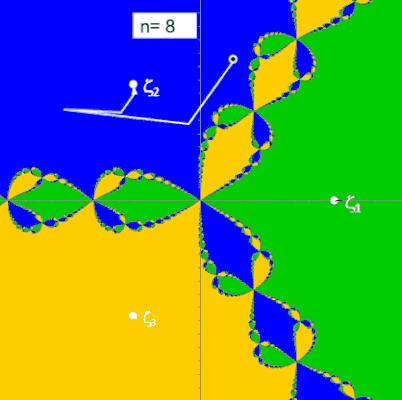
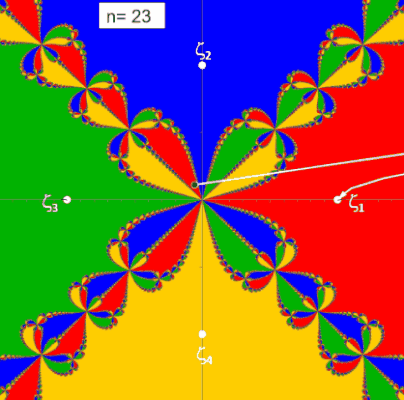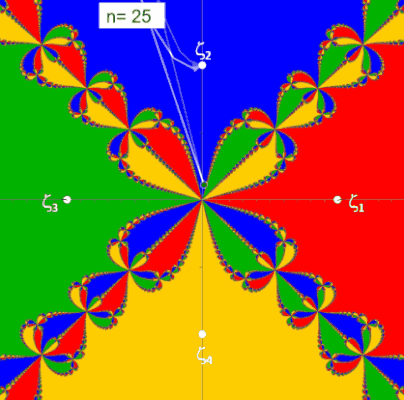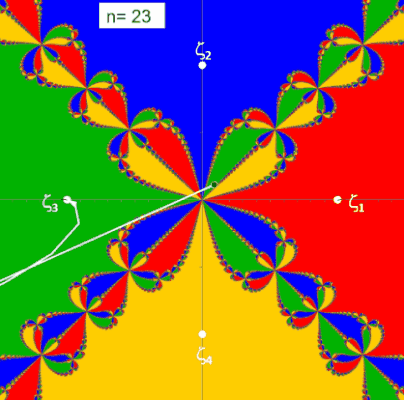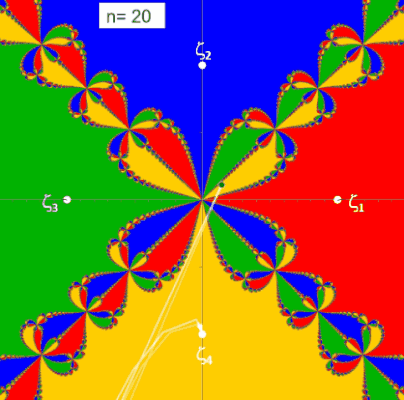
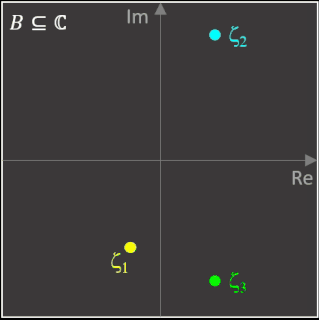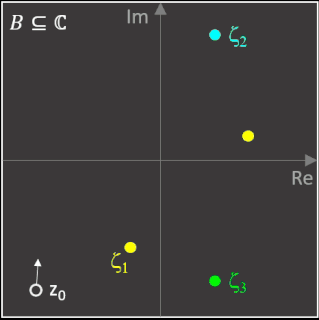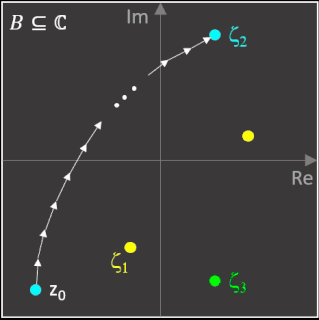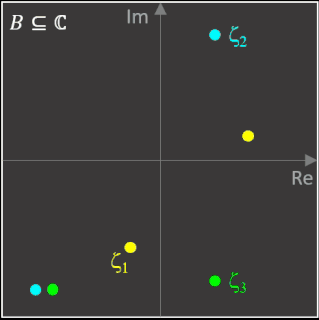
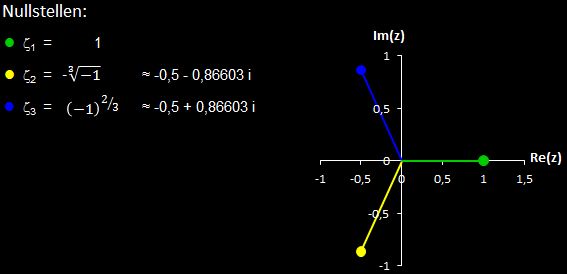
Die folgenden beiden Animationen zeigen für die Funktion z³ - 1 (links) und z4 - 1 (rechts) mit den Nullstellen ζ1, ζ2, ζ3 bzw. ζ1, ζ2, ζ3, ζ4 die mit dem Newton-Verfahren entstehenden Orbits (weißer Streckenzug). Hier überfährt z0 (schwarzer Punkt mit weißem Rand) einen kleinen Bereich von B. Der Wert n ist die Iterationstiefe und gibt an, nach wie vielen Schritten ausgehend von z0 eine Nullstelle ζk erreicht wird.
(Hinweis: Das "fertige" Fraktal mit allen Basins of Attraction (s. folgender Algorithmus) wurde zur Orientierung in der Grafik hinterlegt.)
Berechnung und Darstellung der Basins of Attraction
Für die Berechnung und Darstellung der Basins of Attraction für einen Bereich B ⊆ ℂ der Definitionsmenge einer komplexen Funktion f (z) wird zunächst jeder Nullstelle ζk von f eine eigene Farbe zugeordnet, wie z.B. ζ1 : █ ζ2 : █ ζ1 : █.
Dann wird für jedes z0 ϵ B ein Iterationsverfahren mit z0 als Startwert ausgeführt. Der Startwert z0 ϵ B erhält dann die Farbe der Nullstelle ζk , gegen die die Iteration konvergiert (s. auch folgende Animation) bzw. die Farbe Schwarz im Falle der Divergenz des Verfahrens. Hier der zugehörige Algorithmus in Pseudocode:
Algorithmus I - Basins of Attraction
Man beachte, dass die Nullstellen ζ1, ... , ζk (im Algorithmus sind diese in der Liste Z [ ] enthalten) bekannt und hinreichend genau vorgegeben sein müssen.
Führt man den obigen Algorithmus für reelle Funktionen f : D ⊆ ℝ → ℝ und dem Newton-Verfahren zur Berechnung der Einzugsbereiche für einen Bereich B
⊆ ℝ (Intervall der x-Achse) durch, so erhält man in B farbige Teillinien, wie die folgenden zwei Beispiele zeigen (zur besseren Sichtbarkeit wurde die
x-Achse "verbreitert").
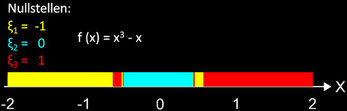
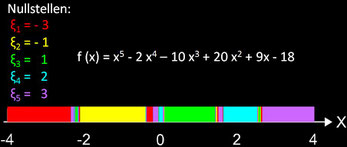
Es zeigt sich, dass die gefundenen Nullstellen nicht in der größenmäßigen Reihenfolge auftreten - was man vielleicht erwarten würde - sondern dass es vielmehr zu Sprüngen und somit zu Farbwechseln kommt. Zommt man in ein Teilintervall von B hinein, in dem Sprünge / Farbwechsel stattfinden, so erhält man auch in diesem Teilintervall wieder weitere Teilintervalle, in denen erneut Sprünge / Farbwechsel stattfinden (vgl. Newton-Verfahren).
Wie sieht nun die entsprechende Grafik für komplexe Funktionen aus?
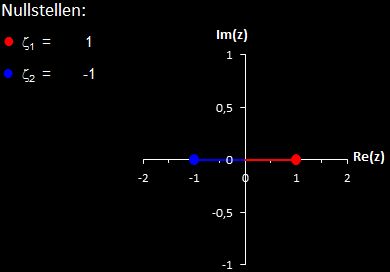
Wendet man z.B. das Newton-Verfahren auf die komplexe Funktion f (z) = z² - 1 an (diese hat nur die beiden reellen Nullstellen 1 und -1), so ist das entstehende Bild der Einzugsbereiche z.B. für B [-2, 2] x [-2, 2] eher unspektakulär: es gibt genau zwei Bereiche, die durch die Imaginärachse exakt begrenzt sind:
Für andere Verfahren (s. unter Basins of Attraction für z^2-1=0) und im Fall
komplexer Funktionen mit drei oder mehr Nullstellen zeigt der Plot für einen Bereich B ⊆ ℂ jedoch ein Fraktal [1] mit mehreren farbigen Teilbereichen in B, wie im
folgenden Beispiel mit dem komplexen Newton-Verfahren und der Funktion
f (z) = z³ - 1 für den Bereich B = [-2, 2] x [-2, 2].
Das Newton-Verfahren konvergiert fast immer gegen eine der drei Nullstellen ζ1, ζ2, ζ3, unabhängig davon, welcher anfängliche Startwert z0 gewählt wird. Ähnlich wie beim reellen Verfahren (s. o.) ist es in einigen Regionen von B jedoch ziemlich unvorhersehbar, welche Nullstelle das sein wird.
Zwischen den drei, jeweils einer Nullstelle zugeordenten "Hauptbereichen" gibt es keine geradlinige, scharfe Grenze, sondern tropfenförmige Strukturen, die wiederum alle drei Farbbereiche enthalten. Durch das Zoomen in kleinere Bereiche werden mehr Details sichtbar, wobei stets wieder die tropfenförmigen Strukturen auftauchen (Selbstähnlichkeit). Beim folgenden Video erfolgt ein Zoom-In bis zu einer Vergrößerung von 50 Millionen.
Die Grenze zwischen den verschiedenen Basins of Attraction scheint Null zu sein, sie ist jedoch unendlich komplex. Es ist absolut unmöglich, im uns zugänglichen Universum eine exakte Zeichnung anzufertigen, wenn man von einer kleinstmöglichen Längenskala in der Größenordnung der Planck-Länge ausgeht. Jedes Mal, wenn man versucht, näher an einen Ausschnitt heran zu zoomen, löst sich dieser in einer unscharfen Struktur mit immer mehr Details auf.
Darstellung der Konvergenzgeschwindigkeit
Eine andere Art der Darstellung zeigt für eine Funktion f die Konvergenzgeschwindigkeit für jeden Punkt
z0 ϵ B beim jeweilig angewandten Iterationsverfahren. Hierbei wird, ausgehend vom Startwert z0 , solange iteriert, bis die Abbruchbedingung |zi - zi-1 | ≤ ε erfüllt ist. z0 ϵ B wird dann die Farbe einer vorgegebenen Farbpalette zugeordnet, wobei der letzte Wert des Iterationsindexes i die Position in der Farbpalette angibt:

Wie auch beim obigen Algorithmus wird z0 ϵ B die Farbe schwarz zugeordnet, falls die maximale Iterationsanzahl erreicht wird. Hier der zugehörige Algorithmus in Pseudocode:
Algorithmus II - Konvergenzgeschwindigkeit
Die Größe/Länge P der Farbpalette kann zwar beliebig sein, jedoch hat sich eine Größe/Länge von P=256 bei vielen Programmen zur Erzeugung von Fraktalen etabliert.
Der letzte Iterationswert i kann für die Punkte z0 ϵ B sehr verschiedene Größenordnungen annehmen. Bei insgesamt sehr kleinen Werten für i (für das Beispiel z³-1=0 liegen für das Newton-Verfahren die meisten Werte unter 25, s. dazu auch die Animation am Anfang dieser Seite) sieht man bei der vorgegebenen Regenbogen-Palette kaum Unterschiede, wie im linken Bild der folgenden Galerie zu sehen ist. Mittels p_step können die Werte von i entlang der Palette "gestreckt" werden (s. mittleres Bild in folgender Galerie mit p_step=10).
Um z0 auch für Werte von i > P einfärben zu können, wird eine Modulo-Berechnung mit der Palettenlänge P durchgeführt, d.h. die Farbwerte wiederholen sich für Werte von i > P. Alternativ kann man die Einfärbung auch so vornehmen, dass Stufen bei der Einfärbung entstehen (s. rechtes Bild in folgender Galerie).
Mit dem Algorithmus II, dem Newton-Verfahren und der obigen Regenbogen-Palette ergeben sich so für die Funktion f (z ) = z³ - 1 für B = [-2, 2] x [-2, 2] folgende Fraktale:
Download
Für den interessierten Leser liegt hier ein EXCEL-Sheet bereit, mit dem auch die Animation zu den Orbits am Anfang der Seite erstellt wurde. Mit Hilfe von Schiebereglern kann die Position von z0 innerhalb B verschoben werden. Ich habe bewusst auf eine "elegante" Programmierung mit VBA und Macros verzichtet, damit die Datei problemlos in den verschiedenen Programmversionen ausgeführt und inhaltlich leicht nachvollzogen werden kann.