VOC - Tool zur Berechnung und Darstellung
Die Berechnung der Basins of Attraction mit Programmen in gängigen Programmiersprachen (z.B. Visual Basic, C, ...) und Ausführung auf der CPU kann auf Grund der häufig sehr langen Rechenzeiten recht frustierend sein.
Eine deutlich vorteilhaftere Alternative ist es, die Berechnungen auf der GPU (!) der Grafikkarte durchzuführen. Dies ermöglicht die freie Schnittstelle OpenGL [1]; mit der Programmiersprache OpenGL SL [2], [3] können dann sog. Shader zur Ausführung auf der GPU programmiert werden.
Im Vergleich zu CPU-basierten Berechnungen sind auf der GPU ablaufende Shader extrem schnell. Dazu hier ein kleines Beispiel ...
Für das rechts abgebildete und häufig im Internet dargestellte "Newton-Fraktal", das sich als Lösung der Gleichung z³ - 1 = 0 ergibt (s. Basins of Attraction z^3-1=0), ergeben sich bei gleichem Bereich B und gleicher Iterationstiefe für meine derzeit verwendete recht schnelle Hardware (s. Diverse Themen / Tools) folgende Rechenzeiten :
- Standard-Berechnung (CPU): 21.1 Sekunden für 1024 x 1024 Pixel
- OpenGL Shader (GPU): 0.26 Sekunden für 1024 x 1024 Pixel
Dies entspricht einer ca. 80-fach schnelleren Berechnung mit dem Shader. Hierdurch sind auch Animationen in Echtzeit möglich.

Auf der Suche nach einer geeigneten Programmierumgebung fand ich die kostenlose (!) Software
Visions of Chaos (VOC) von Softology [4], die verschiedenste Aspekte und Methoden zur Berechnung von Chaos unter einem Dach vereint und dem Anwender ein großes
Feld für eigene Experimente und Darstellungsarten erschließt.
In der Software sind unter Rootfinding Fractals bereits einige komplexe Polynome, 5 Iterationsverfahren sowie einige Möglichkeiten der "künstlerischen Aufbereitung / Verfremdung" der Fraktale vorhanden.
Der Clou aber ist der, dass der Author Jason Rampe in seiner Software auch eine Schnittstelle/Editor für OpenGL SL zur Verfügung stellt. Hierdurch hat man die Möglichkeit, eigene Shader zu programmieren, um so beliebige Polynome, Iterationsverfahren, Methoden der Einfärbung zu testen oder Animationen zu erstellen.
Insbesondere konnte ich so auch die Erzeugung von Fraktalen mit trigonometrischen und Exponentialfunktionen programmieren.
Komplexe Arithmetik in OpenGL SL
Die Programmiersprache OpenGL SL, in der die Shader (.CFF-Dateien) erstellt werden, verfügt leider nicht den Datentyp "Complex" und bietet folglich auch keinerlei Rechenoperationen für komplexe Zahlen! Rechenoperationen für komplexe Zahlen müssen daher selbst mit den vorhandenen Funktionen für reelle Zahlen programmiert werden.
Für die Grundrechenarten Addition, Subtraktion, Multiplikation, Division und die Quadratwurzel komplexer Zahlen a, b
∈ ℂ mit a = ax + i • ay und b = bx + i • by gelten folgende Rechenregeln:
Für die Implementierung komplexer Zahlen in OpenGL SL bietet es sich an, komplexe Zahlen als zweidimensionale Vektoren zu definieren:
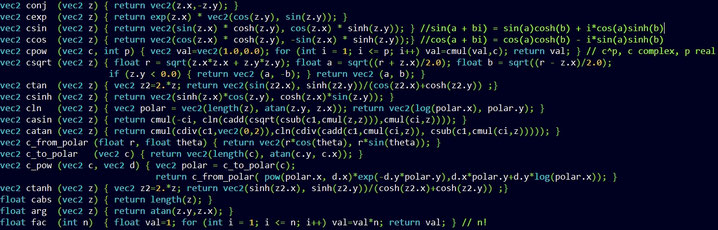
Die obigen Rechenarten habe ich folgendermaßen in OpenGL SL implementiert:
Da die Grundrechenarten in OpenGL SL in doppelter Genauigkeit (double bzw. dvec) bereitstehen, gilt dies auch für die obigen komplexen Rechenarten.
Die komplexe Exponentialfunktion cexp (z), komplexe Sinusfunktion csin(z) und komplexe Cosinus-Funktion ccos(z) mit z ϵ ℂ habe ich wie folgt umgesetzt:
- cexp (z) = ez = ex+i y = ex ei y = ex [ cos (y) + i sin (y) ] mit z = x + i y ϵ ℂ
- csin (z) = sin (x +i y) = sin (x) cosh (y) + i cos (x) sinh (y) mit z = x + i y ϵ ℂ
- ccos (z) = cos (x + i y) = cos (x) cosh (y) - i sin (x) sinh(y)
- csinh (z) = ½ (ez - e-z)
Hierbei sind ex, sin , cos, sinh, cosh die in OpenGL SL vorhandenen reellwertigen Funktionen. Diese sind in OpenGL SL nur in einfacher Genauigkeit (float bzw. vec2) implementiert:

Shader, bei denen diese Funktionen genutzt werden, können daher leider nur in einfacher Genauigkeit programmiert werden!
Dies führt bei der Berechnung der Basins of Attraction komplexer Exponential-, trigonometrischer und hyperbolischer Funktionen zum einen dazu, dass bei größeren Zoom-Werten die berechneten Bilder schnell pixelig werden können. Zum anderen muss auf Grund der geringen Rechengenauigkeit bei den meisten Iterationsverfahren die Toleranzschwelle ε (s. Grundlagen und Algorithmen) deutlich erhöht werden.
Verwendung der bereitgestellten Shader (.CFF-Dateien)
Für die Beispiele unter Basins of Attraction stehen jeweils im Download-Bereich Shader (.CFF-Dateien) zum Runterladen und schnellen Berechnung mit VOC zur Verfügung.
Laden Sie dazu zunächst das VOC Tool runter [4].
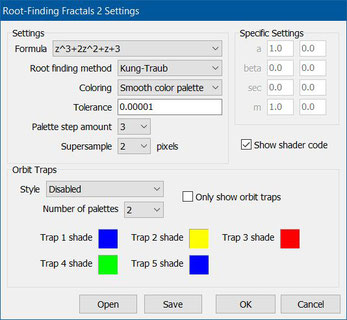
Wählen Sie nach dem Start von VOC das Menü OpenGL Shading Language / Custom Formular Editor (s. rechte Abbildung).
Im sich öffnenden Fenster kann dann mittels Klick auf den Button Open die gewünschte .CFF-Datei geladen und durch Klick auf den OK-Button ausgeführt werden.
13.03.2021 - Nachtrag
Inzwischen hat sich eine "fruchtbare" Zusammenarbeit mit Jason Rampe, dem Autor von VOC, ergeben (s. auch in diesem Blog): die auf meiner Seite bis dato beschriebenen Iterationsverfahren
- Newton-Verfahren
- Halley-Verfahren
- Schröder-Verfahren
- Householder-Verfahren
- Basto-Verfahren
- Whittaker I -Verfahren
- Whittaker II -Verfahren
- Euler-Chebyshev-Verfahren
- Chun-Kim I -Verfahren
- Sekanten-Verfahren
- Ostrowski-Verfahren
- King-Verfahren
- Chun II-Verfahren
- Chun III -Verfahren
- Feng-Verfahren
- Contra Harmonic Newton-Verfahren
- Kung-Traub-Verfahren
- Fang-Ni-Cheng-Verfahren
- Rafiq-Rafiullah-Verfahren
- Chun-Kim II -Verfahren
- Chun-Kim III -Verfahren
- Sharma-Bahl-Verfahren
- Chun-Lee-Neta-Verfahren
wurden in VOC eingebaut und stehen nun für eine Vielzahl von Polynomen dem Anwender zum eigenen Experimentieren zur Verfügung.
Hier das aktuelle Eingabefenster für die gewählte Funktion z³ + 2 z² + z + 3 und das Kung-Traub-Verfahren sowie das generierte Fraktal:
Die Fraktale werden nun nicht mehr wie in früheren Versionen von VOC mit der CPU, sondern nun mit der GPU berechnet - ein Riesenschritt in Sachen Geschwindigkeit!
Dazu wird entsprechend den Vorgaben im Eingabefenster ein Shader erzeugt und ausgeführt; dieser kann sogar angezeigt, modifiziert und gespeichert werden.
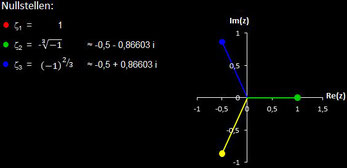
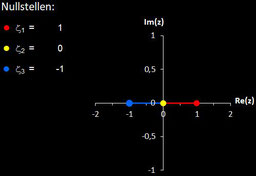
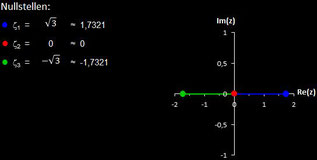
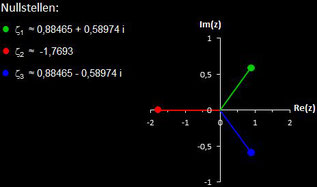
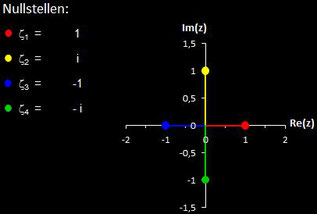
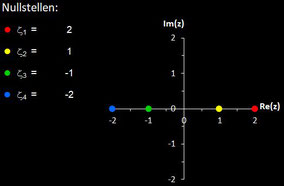
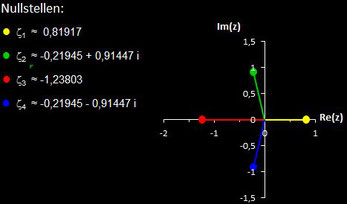
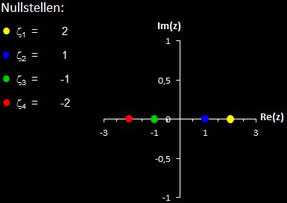
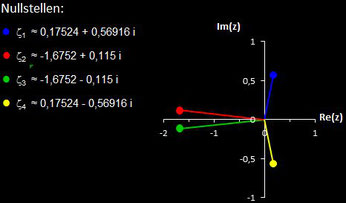
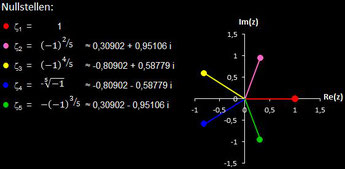
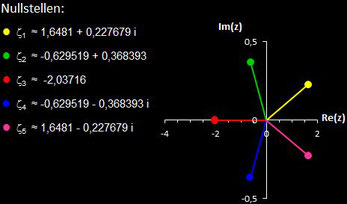
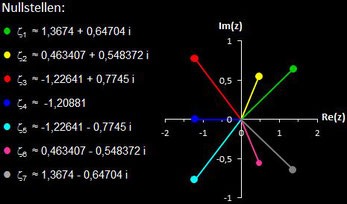
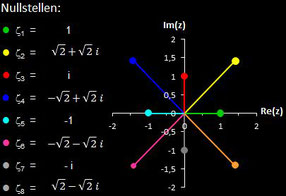
Polynome und ihre Nullstellen in VOC
Im folgenden habe ich für die in VOC fest implementierten Polynome deren Nullstellen berechnet.