Schröder-Verfahren

Im Jahr 1870 publizierte E. Schröder ein modifiziertes Newton-Verfahren, das auch im Falle mehrfacher Nullstellen eine quadratische Konvergenz besitzt [1]:

und das man herleiten kann, indem man die Funktion f ersetzt durch die Funktion

Dort, wo f mehrfache Nullstellen besitzt, hat u_f  jeweils nur eine einfache Nullstelle. Durch die zusätzliche Berechnung von f '' verringert sich die Effizienz gegenüber dem Newton-Verfahren auf den Wert CE = 1.2599.

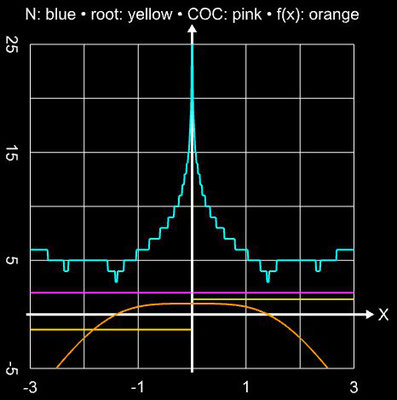
Angewandt auf die Beispielfunktion (s. Diverse Verfahren) f (x) = sin ² (x) - x² + 1 mit ihren beiden Nullstellen
ξ₀ ≈ -1.404491648215341226 und ξ₁ ≈ 1.404491648215341226 ergibt sich für COC exakt der Wert 2:

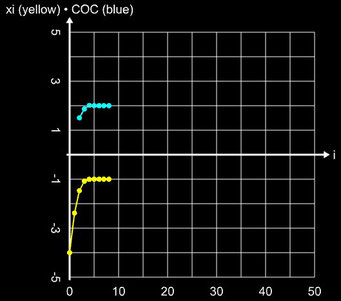
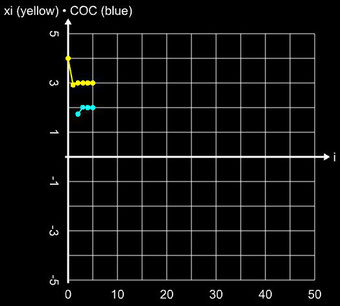
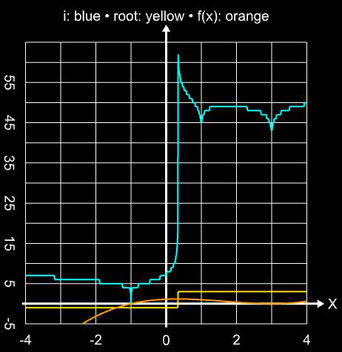
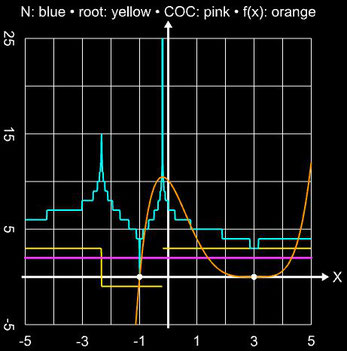
Als Beispiel für das unterschiedliche Konvergenzverhalten des Newton- und Schröder-Verfahrens betrachte man die Funktion f (x) = 0.125 (x+1) (x-3) ². Sie besitzt die einfache Nullstelle ξ₁ = -1 sowie die doppelte Nullstelle ξ₂ = 3. Als Abbruchkriterium bei den Iterationen wurde | x_i – x_i-1 | + | f(x_i) | ≤ 10^-15 gewählt.

Einfache Nullstelle, x₀ = - 4:

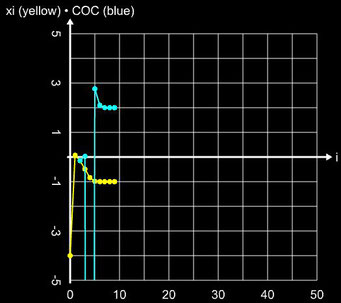
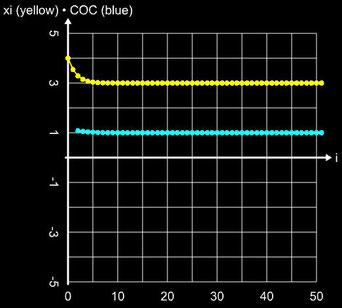
Doppelte Nullstelle, x₀ = 4:

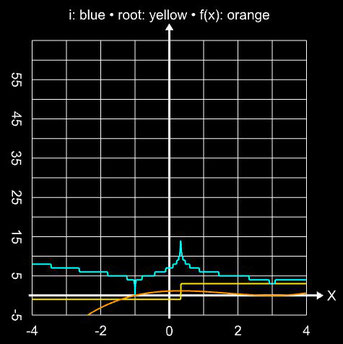
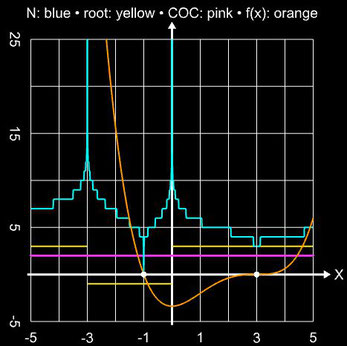
Einzugsbereiche:

Nachfolgend zwei Beispiele mit einer Kombination aus je einer einfachen Nullstelle bei ξ₁ = -1 und dreifachen bzw. vierfachen Nullstelle bei ξ₂ = 3. In beiden Fällen liegt der Wert für COC bei 2.0000...

Quellenverweise

[1]   E. Schröder, Ueber unendliche viele Algorithmen zur Auflösung der Gleichungen,
       Mathematische Annalen, Band 2 (1870), S. 317