Nullstellenbestimmung - Verfahrensvergleich

Die Besonderheiten der auf meiner Webseite betrachteten vier Verfahren Sekanten-, Newton-, Tiruneh- und Halley-Verfahren zur Bestimmung der Nullstellen einer reellen Funktion sind in folgender Tabelle zusammengestellt.
Im folgenden wird für einige Funktionen das unterschiedliche Verhalten der Verfahren dargestellt ...
• f (x) = x5 - 3x4 - 5x3 + 15x2 + 4x -
12
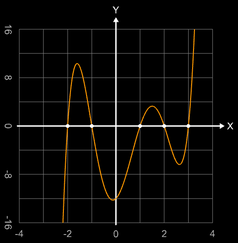
Das Poylnom hat die einfachen Nullstellen {-2, -1, 1, 2, 3}.
Sekantenverfahren
Newton-Verfahren
Halley-Verfahren
• f (x) = x3 - 2x + 1
Sekantenverfahren
Newton-Verfahren
Halley-Verfahren

