Wilbraham-Gibbs Konstante
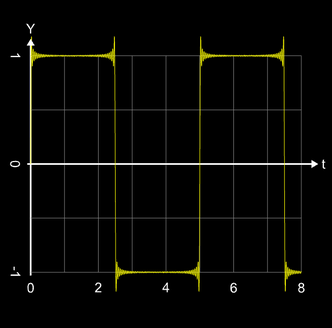
Entwickelt man eine Fourierreihe für eine unstetige Funktion, d.h. die Funktion weist Sprungstellen auf, wie z.B. eine Rechteckschwingung, so ergeben sich an den Sprungstellen (Unstetigkeitsstellen) typische Über- und Unterschwinger (s. Grafik rechts).
Dieses Verhalten wird als Gibbs'sches Phänomen bezeichnet (s. Beispiele dazu bei Additive Synthese von Wellenformen).
Dieser Fehler ist von prinzipieller Art, d.h. er ließe sich auch nicht vermeiden, wenn man unendlich viele Summanden berücksichtigen würde. Durch eine Erhöhung der
Anzahl der Summanden wird zwar der fehlerhafte zeitliche Bereich enger, nicht jedoch die maximale Abweichung der Über- und Unter-schwingungen.
Es lässt sich zeigen [1], dass die Höhe der Über-/Unterschwinger einem Grenzwert entgegenstrebt:
Dieser Wert wird Wilbraham-Gibbs Konstante genannt.
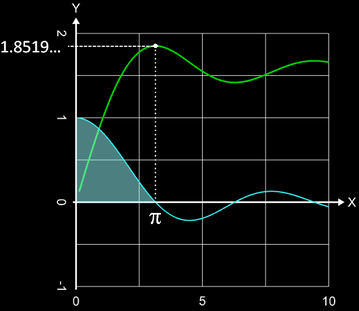
Bei der Berechnung des Integrals Si (π) (s. Grafik rechts und auch unter Integralsinus) mit Graphing Calculator 3D ist zu beachten, dass die zu integrierende Funktion an der unteren Grenze x = 0 nicht definiert ist und man sich der Stelle nur annähern kann.
Wählt man als untere Integralgrenze a = 10-15
und
n = 4000, so erhält man mit 14-stelliger Genauigkeit Si (π)
= 1.85193705198246...
Dies gilt auch für die berechnete Wilbraham-Gibbs Konstante: 1.17897974447216 ...
Noch genauere Werte lassen sich ermitteln, indem man statt der mathematischen Standardbibliothek die Bibliothek "APfloat" wählt, wobei sich jedoch die Rechenzeit drastisch erhöht.
