Polysphericons - Grundlagen
Die Basis für die weiteren Betrachtungen bildet das erstmals 1969 von Colin Roberts beschriebene Sphericon, - quasi das "Ursphericon" - das auf einem Quadrat beruht [1]. Dessen Bauprinzip folgend, kann eine Reihe unterschiedlicher Sphericons (sog. Polysphericons) für p, k ∈ ℕ, p ≥ 3, 0 ≤ k < p konstruiert werden:
- Bilde den Rotationskörper eines regulären p-Ecks mit p > 2
- Halbiere diesen entlang eines p-Ecks
- Rotiere eine Hälfte k ∙ 2π / p um die durch den Mittelpunkt des Polygons verlaufende Achse
- Setze beide Hälften wieder zusammen: es entsteht ein (p, k)-Polysphericon.
Das (p, 0)-Polysphericon ist der Rotationskörper vor Halbierung und Drehungen.
Flächen und Kanten
Abhängig vom Grundpolygon (gerade oder ungerade Anzahl der Ecken) und der Lage der Rotationsachse (Ecke-Ecke, Ecke-Kante, Kante-Kante) kann man jedem Körper eine Klasse von Polysphericons zuordnen:
- Duales Polysphericon: p ist gerade, Rotationsachse Kante-Kante
- Gerades Polysphericon: p ist gerade, Rotationsachse Ecke-Ecke
- Ungerades Polysphericon: p ist ungerade, Rotationsachse Ecke-Kante
Aus der Anzahl p der Ecken und Anzahl k der Drehungen einer Hälfte mit 0 ≤ k < p lässt sich die jeweilige Anzahl der Flächen und Kanten des Polysphericons bestimmen:
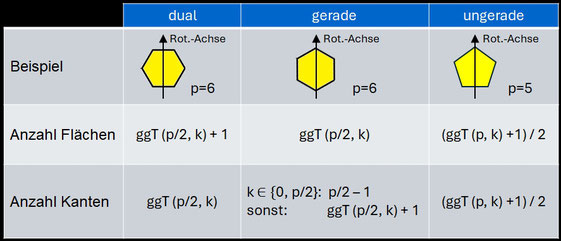
Daraus lassen sich direkt die folgenden Aussagen für geradzahliges p ableiten.
- Auf der Grundlage geradzahliger Polygone lassen sich nur exakt p / 2 unterschiedliche Polysphericons erzeugen lasssen, wobei der ursprüngliche Rotationskörper (k = 0) darin enthalten ist. Für geradzahliges p gilt die folgende Identität:
(p, k)-Polysphericon ≡ (p, k mod p/2)-Polysphericon mit 2 < k < p
- Die Anzahl der Flächen eines dualen (p, k)-Polysphericons ist stets um den Wert eins größer als die des geraden (p, k)-Polysphericons.
Für die auf meiner Seite betrachteten Polysphericons zeigt die folgende Tabelle die konkreten Werte für die Anzahl der Flächen und Kanten. Bei einem Wert von k = 0 wird die Anzahl der Flächen und Kanten des Rotationskörpers vor dessen Halbierung und Drehung angegeben. Für die Färbung gilt:
- lila unterlegte Felder: Werte für gerade Polysphericons (Rotationsachse Ecke - Ecke)
- orange unterlegte Felder: Werte für duale Polysphericons (Rotationsachse Kante - Kante).
|
Trisph. p = 3 |
Tetrasp. p = 4 |
Pentasph. p = 5 |
Hexasph. p = 6 |
Heptasp. p = 7 |
Octasph. p = 8 |
Nonasphericon p = 9 |
Dodecasphericon p = 12 |
|||||||||||||||||||||
|
k: |
0 3 |
1 | 2 |
0 2 4 |
1 3 |
0 5 |
1...4 |
0 3 6 |
1 4 |
2 5 |
0 7 |
1...6 |
0 4 8 |
1 5 |
2 6 |
3 7 |
0 9 |
1 2 |
3 |
4 5 |
6 |
7 8 |
0 6 12 |
1 7 |
2 8 |
3 9 |
4 10 |
5 11 |
| Flächen | 2 | 1 | 1 | 2 | 1 | 3 | 1 | 3 | 1 | 1 | 4 | 1 | 4 | 1 | 2 | 1 | 5 | 1 | 2 | 1 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 |
| 3 | 2 | 4 | 2 | 2 | 5 | 2 | 3 | 2 | 7 | 2 | 3 | 4 | 3 | 2 | ||||||||||||||
| Kanten | 1 | 1 | 1 | 1 | 2 |
2 |
1 | 2 | 2 | 2 | 3 | 1 | 3 | 2 | 3 | 2 | 4 | 1 | 2 | 1 | 2 | 1 | 7 | 2 | 3 | 4 | 3 | 2 |
|
2 |
1 | 3 | 1 | 1 | 4 | 1 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 | ||||||||||||||
Aus den obigen Formeln leiten sich für ungerade als auch für gerade Polysphericons die folgenden Aussagen zur Anzahl der Flächen eines (p, k)-Polysphericons mit 0 < k < p ab; die Bedingungen für gerade Polysphericons sind lila unterlegt.
- Ist p (p/2) prim, so haben alle (p, k)-Polysphericons jeweils genau eine Fläche.
Beispiele:
p ungerade: Tri-, Penta-, Heptasphericon (s. Tabelle oben),
p gerade, p ≠ p/2: Hexasphericon (s. Tabelle oben),
- Ist p = n² (p/2 = n²) und n ist prim, so hat jedes (p, k)-Polysphericon mehr als eine Fläche, falls k ein Vielfaches von n ist; für alle anderen k-Werte hat es genau eine Fläche.
Beispiele:
p ungerade: Nonasphericon,
p gerade: Octasphericon,
- Ist p (p/2) nicht prim, sondern p lässt sich vollständig in die Primfaktoren p1, …,pn zerlegen, so hat das (p ,k)-Polysphericon mehr als eine Fläche, falls k gleich oder ein Vielfaches einer der möglichen Kombinationen ohne Wiederholung der n Primfaktoren ist; für alle anderen k-Werte hat es genau eine Fläche.
Beispiel: p (p/2) = 105 = 3 • 5 • 7
Rollt es oder rollt es nicht - abwickelbare Walzen
Einige der oben aufgeführten Polysphericone sind abwickelbare Walzen [2], d.h. sie sind konvex gekrümmte, dreidimensionale Körper, die auf einer ebenen Fläche endlos ohne Unterbrechung abrollen können, so dass letztlich jeder Punkt ihrer Oberfläche die Ebene berührt.
Es gilt: Ein gerades (p , k)-Polysphericon ist eine abwickelbare Walze genau dann, falls ggT (p/2, k) = 1
(s. dazu auch obige Tabelle).
Ein rollendes Sphericon finden Sie unter Sphericon. Die folgende Videosequenz zeigt das Rollen eines (6,1)-Hexasphericons [3].
Ein Polysphericon mit ungeradem p ist hingegen niemals eine abwickelbare Walze. Es kann zwar eine einzelne abwickelbare Fläche besitzen, rollt aber nicht unbegrenzt, da der Rotationskörper eine kreisförmige Fläche hat, an der die Rotationsachse eine Kante schneidet, was zu Sackgassen führt, die das Rollen des Polysphericons verhindern. Dies erkennt man z.B. unmittelbar beim (3,1)- oder (3,2)-Trisphericon oder beim dualen (4,1)-Tetrasphericon.
Sehr schöne Animationen zum Abrollen der Fläche vom Tri-, Penta- und Heptasphericon kann man sich bei [4] ansehen.
Das zuvor Gesagte gilt auch für duale Polysphericons. Sie besitzen entweder mehrere separate Flächen, sodass sie abrupt stoppen, oder aber sie rollen im Kreis wie ein Kreisel, dem die Energie ausgeht. Bei [5] (weiter unten auf der Seite) finden Sie hierzu ein Video.
Quellenverweise
[1] https://en.wikipedia.org/wiki/Sphericon
[2] https://polytope.miraheze.org/wiki/Developable_roller#Prime_polysphericons
[3] https://discourse.mcneel.com/t/designing-a-hexasphericon/87141/5
[4] https://www.youtube.com/watch?v=XdSZ4Ubrd0c
[5] https://altdynamic.com/shop/the-hexasphericon-point-type

![rollendes (6,1)-Hexasphericon [3]](https://image.jimcdn.com/app/cms/image/transf/dimension=501x10000:format=gif/path/scee86bccd27a6ab2/image/i4bb68afab9824779/version/1749632498/rollendes-6-1-hexasphericon-3.gif)