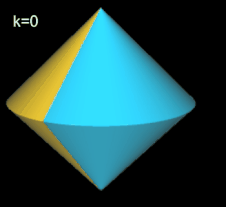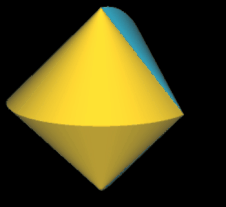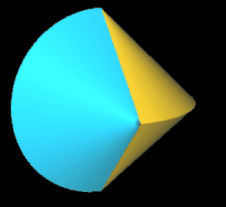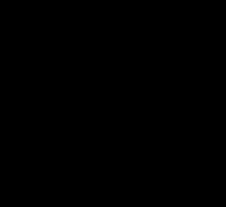
Tetrasphericon (p=4)
Gerades Tetrasphericon ≡ Sphericon
Das gerade Tetrasphericon ist das "Ursphericon"; weitere Informationen finden Sie auf der Seite Sphericon.
Für die Flächen und Kanten gilt folgender Zusammenhang:
|
Gerades Tetrasphericon ≡ Sphericon p = 4 |
|||
| k: |
0 2 |
1 3 |
|
| Flächen | 2 | 1 | |
| Kanten | 1 | 2 | |
Außerdem sind das gerade (4, 1)-Tetrasphericon und das gerade (4, 3)-Tetrasphericon identisch.
Duales Tetrasphericon
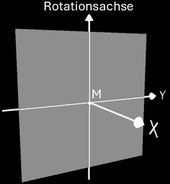
Der zugrunde liegende Rotationkörper beim dualen Tetrasphericon, ein Zylinder, entsteht durch die Rotation eines Quadrats der Seitenlänge a um eine Achse durch die Mitte zweier gegenüberliegender Seiten (s. folgende Grafik). Eine Hälfte des durch Rotation entstandenen Zylinders kann dann um Winkelschritte von π / 2 gedreht werden.
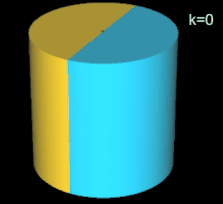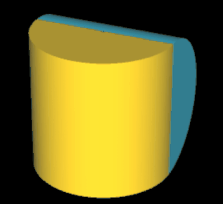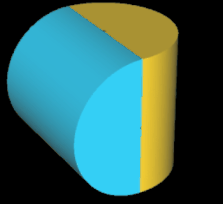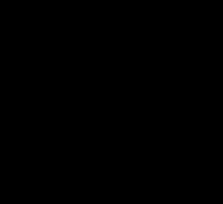
Die folgende Tabelle zeigt den Zusammenhang von Flächen und Kanten in Abhängigkeit der Drehungen. Das duale (4, 1)-Tetrasphericon und duale (4, 3)-Tetrasphericon sind identisch.
Hinweis: Um die Entstehung des Tetrasphericons besser beobachten / nachvollziehen zu können, sind in der folgenden Animation die beiden Hälften des Rotationskörpers unterschiedlich eingefärbt. Nach der Drehung wurden die beim erzeugten Tetrasphericon entstandenen Flächen (2) neu (grau/grün) eingefärbt.
Das Volumen und die Oberfläche des dualen Tetrasphericons errechnen sich zu: