r1 = r2 , r1² ≠ q² , D ≠ 0
r1 = r2 = q , r1 D p ≠ r1 p²
q = 0 , r1 D + r2 p ≠ r1 p
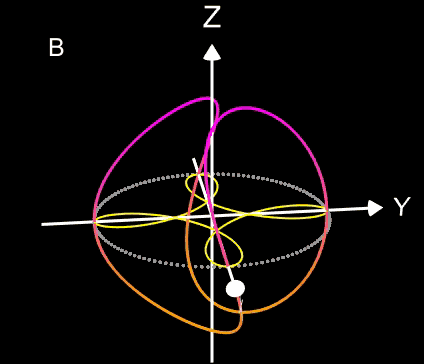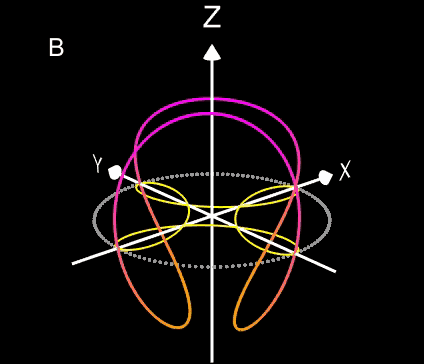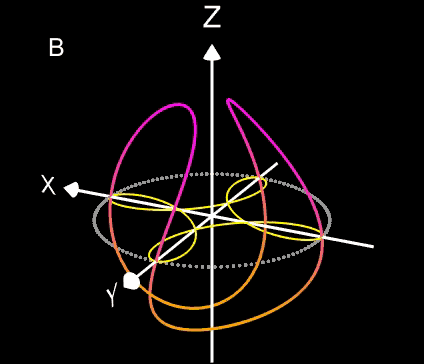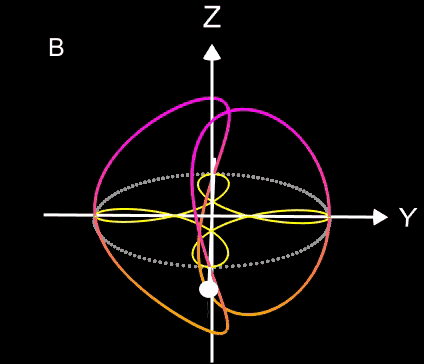
Wie auch bei der vorherigen Problemstellung beträgt der minimal mögliche Radius Rmin des Kreisbogens ½ (r1+D+r2), d.h. Q liegt bei diesem Wert für dann auf dem Umkreis mit Radius Rmin. (blau in obigen Grafiken). Liegt Q nah am Tangentenabschnitt t, so kann R sehr große Werte annehmen bis hin zu ∞, falls Q genau auf t liegt.
Zur Berechnung des Radius R und des Mittelpunktes M des Kreisbogens b habe ich bisher noch keinen Zusammenhang in geschlossener Form aufstellen können. :-((
Vielleicht hilft ja jemand aus der Leserschar?
Eine vorläufige Lösung ist die Iteration von R, d.h. ausgehend von Rmin wird R erhöht, bis die Strecke MQ ungefähr gleich groß wie R ist. Die folgenden Animationen zeigen dazu ein paar Beispiele, wobei der Punkt Q sich auf verschiedenen Wegen durch die Bereiche I bis III bewegt. Der erscheinende "einsame" cyan-farbene Punkt ist der Mittelpunkt M des Kreisbogens b.
Die folgende Fläche mit dem definierenden Polynom f (x, y, z) = -x³ - y² z - x z² + x z = 0 besitzt die zwei Singularitäten P (0 | 0 | 0) und Q (0 | 0 | 1).
Es gilt:
f (P) = f (Q) = 0

Klicken Sie auf ein Bild für eine größere Ansicht.
komplexe Funktion f : D → W mit D, W ⊆ ℂ

Hierzu ein Beispiel:
f (x) = x³ + x² - 17 x + 15, bestimme die Nullstellen
- f (x) = 0
- rate Lösung: x0 = 1 f (1) = ... = 0 o.k.
- Polynomdivision:
(x³ + x² - 17 x + 15) : (x - 1) = x² + 2 x - 15
- (x³ - x²)
2 x² - 17 x
- (2x² - 2 x)
15 x + 15
- (15 x +15)
0
- Restpolynom zu Null setzen und lösen:
x² + 2 x - 15 = 0
...
x1 = 3 x2 = - 5
Das Verfahren der Polynomdivision entspricht im Wesentlichem dem Verfahren des schriftlichen Dividierens zweier Zahlen, wie z.B.
Für meine Schüler(innen) hatte ich einst ein kleines Erklärvideo erstellt, das die einzelnen Schritte bei der Polynomdivision zeigt:



Weitere Berechnungen / Experimente
Falls Sie die obigen Resultate nachvollziehen oder weitere Berechnungen / Experimente mit unterschiedlichsten Parametereinstellungen selbst vornehmen möchten, steht hierfür die nachfolgende ZIP-Datei als Download zur Verfügung. Sie enthält eine .CFF-Datei, die mit dem Programm Vision of Chaos für ca. 50 Iterationsverfahren die Berechnung der Basins of Attraction sowie der Konvergenzgeschwindigkeit (s. dazu Basins of Attraction - Algorithmen) für die entsprechende Funktion ermöglicht.
Für eigene Berechnungen / Experimente mit VOC laden Sie den Shader-B herunter und ersetzen Sie den entsprechenden Abschnitt im Shader-B mit den folgenden Daten (Copy & Paste).

3D Kürbis als Parameterfläche
"... und kam die goldene Herbsteszeit
und die Birnen leuchteten weit und breit..."
Ein-Schritt-Verfahren (one-step methods)









Zwei-Schritt-Verfahren (two-step methods)













Klicken Sie auf ein Bild in der Galerie, um dieses zu vergrößern und den Verfahrensnamen sowie verfahrensspezifische Parameter anzuzeigen. Innerhalb der Galerie bewegen Sie sich mit den Pfeiltasten ← → am linken / rechten Bildschirmrand.
CET Berlin
Frohe Ostern!
CET Berlin


Klicken Sie auf die Steuerelemente
oder die Miniaturansicht, um sich gezielt ein Bild anzuschauen.
Für eine größere, detailreichere Ansicht klicken Sie auf das
Symbol . Für eine noch weitere Vergrößerung klicken
Sie auf die erscheinende Bildschirmlupe
.
Das "Kernstück" ist dabei der Nocken. Dieser wid hier mittels einer "Ei-Kurve" erzeugt. Für die Rotation (s. auch Rotationen im Raum) wird diese jedoch nicht wie beim 3D Ei per "einfacher" Funtion y = f (x) realisiert, sondern als parametrische Funktion [4]:
"... und kam die goldene Herbsteszeit
und die Birnen leuchteten weit und breit..."
Erntezeit ...
3D Apfel als Parameterfläche

Math meets Winter ...
|
01.09.18 - Neue Galerie unter '3D Mathe / 3D Flächen / Parameterflächen'
28.08.18 - Bild-Icons auf einigen Seiten für einfachere mobile Navigation 07.07.18 - 'Spielwürfel' unter '3D Mathe / 3D Objekte' erweitert 16.06.18 - neu: 'Planetensystem' unter '3D Mathe' 09.05.18 - neu: 'Verfahrensvergleich' unter 'Numerische Verfahren/Nullstellen' 05.05.18 - Neue Beispiele beim Sekantenverfahren 29.04.18 - Alternative mit User Library unter 'Integral / Normalverteilung" 23.04.18 - neu: 'Sekantenverfahren' unter 'Numerische Verfahren/Nullstellen' 01.04.18 - Neue Beispiele beim Newton-Verfahren 24.03.18 - neu: 'Newton-Verfahren' unter 'Numerische Verfahren/Nullstellen' 18.03.18 - neu: 'Grundlagen' unter 'Numerische Verfahren/Nullstellen' 05.03.18 - neu: 'Iterationen' unter 'Numerische Verfahren' 02.01.18 - Neue Seitenstruktur |
|
26.08.17 Text
25.08.17 Text 24.08.17 Text 24.08.17 Text 24.08.17 Text 24.08.17 Text 24.08.17 Text |
Beispieldatei.gc3
Das ist ein Schlagwort zum Überfahren mit der Maus.
zum Überfahren mit der Maus.
Das Schlagwort ist ein zum Überfahren mit der Maus.
ist ein zum Überfahren mit der Maus.
Das Schlagwort ist ein zum Überfahren mit der Maus.
ist ein zum Überfahren mit der Maus.
Text
Wenn Sie hier im Text dieses Stichwort mit der Maus überfahren, öffnet sich ein Bild mit einem Erklärtext.
Die Planetenbahnen und die Bahn des Mondes um die Erde sind Ellipsen, wenn auch nahezu kreisförmig. Bei der Bahnberechnung für die Planeten und den Mond wurden außer der mittleren Umlaufzeit folgende Größen berücksichtigt (Werte bei [1]):
große Halbachse • Exzentrizität • Inklination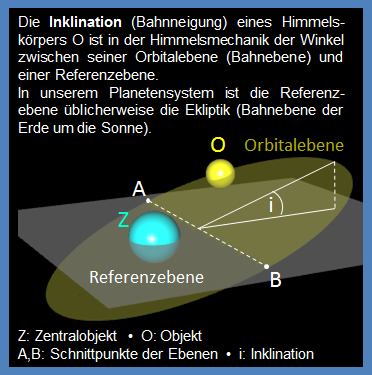 • Achsneigung (bei Erde und Saturn).
• Achsneigung (bei Erde und Saturn).
Die folgende Animation zeigt den Umlauf von Merkur (grau), Venus (orange) und Erde mit Mond um die Sonne für ein Jahr (hier: 2018). Schön zu sehen: durch die Neigung der Erdachse von 23.44° zur Ekliptik (Ebene der Umlaufbahn zur Sonne) entstehen die Jahreszeiten.
Die Planetenbahnen und die Bahn des Mondes um die Erde sind Ellipsen, wenn auch nahezu kreisförmig.
Bei der Bahnberechnung für die Planeten und den Mond wurden berücksichtigt (Werte bei [1]):
- große Halbachse
- Exzentrizität
-
Inklination
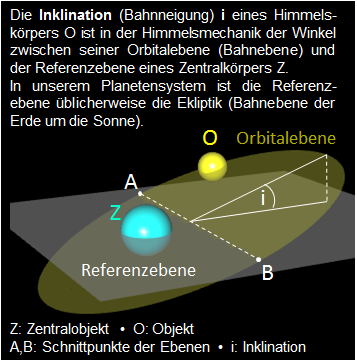
- Achsneigung (bei Erde und Saturn)
- mittlere Umlaufzeit.
Die folgende Animation zeigt den Umlauf von Merkur (grau), Venus (orange) und Erde mit Mond um die Sonne für ein Jahr (hier: 2018). Schön zu sehen: während die Erde die Sonne umläuft, bleibt die Neigung der Erdachse von 23.44° zur Ekliptik (Ebene der Umlaufbahn um die Sonne) im Raum (abgesehen von langperiodischen Effekten) fast unverändert . Dadurch ist von März bis September die Nordhalbkugel etwas mehr zur Sonne hin geneigt, von September bis März die Südhalbkugel. Im Jahreslauf ändern sich daher der Einfallswinkel der Sonnenstrahlen und die Dauer des lichten Tages, womit die Jahreszeiten entstehen.
Die Planetenbahnen und die Bahn des Mondes um die Erde sind Ellipsen, wenn auch nahezu kreisförmig. Bei der Bahnberechnung für die Planeten und den Mond wurden außer der mittleren Umlaufzeit folgende Größen berücksichtigt (Werte bei [1]):
große Halbachse • Exzentrizität • Inklination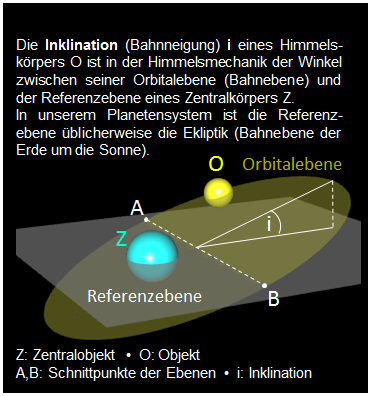 • Achsneigung
• Achsneigung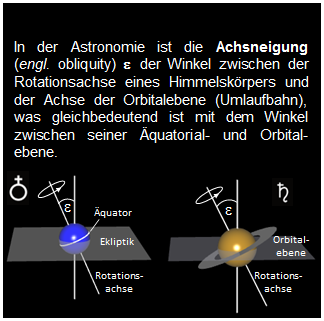 (bei Erde und Saturn).
(bei Erde und Saturn).
Die folgende Animation zeigt den Umlauf von Merkur (grau), Venus (orange) und Erde mit Mond um die Sonne für ein Jahr (hier: 2018). Schön zu sehen: durch die Neigung der Erdachse von 23.44° zur Ekliptik (Ebene der Umlaufbahn zur Sonne) entstehen die Jahreszeiten.
Such tips are called
singularities . Singularities can look very different (especially not necessarily
sharp, see also at the bottom) and appear in many other fields of mathematics, physics, technology and nature.
A point P ( p x | p y | p
z ) of an algebraic surface with the equation f (x, y, z) = 0 is called singularity if both
as well as all partial derivatives of f equal zero are:
Otherwise, P is called smooth .
Whereas for every smooth point of an algebraic surface f a tangential plane exists at this point, since the gradient for f at this point is not (0, 0, 0), this is not the case for a singularity at point P, since for the Gradient at point P holds:
| Integrale | Integralanwendungen | |||||
| Numerische Integration | Doppelintegral | Fläche zwischen Funktionsgraphen | Flächenschwerpunkt zwischen Funktionsgraphen | Länge Funktionsgraph | Normalverteilung | |