Dodecasphericon (p=12)
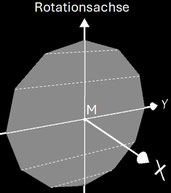
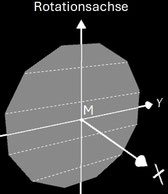
Rotiert man ein regelmäßiges Zwölfeck (Dodecagon) um eine Achse in dessen Ebene, so entsteht der Grundkörper für das Dodecasphericon. Da p = 12 geradzahlig ist, gibt es die zwei Varianten gerades Dodecasphericon und duales Dodecasphericon. Auf Grund der Symmetrie existieren bei beiden Varianten außer dem Grundkörper (k = 0) jeweils nur fünf verschiedene Exemplare. Dabei gelten für beide Varianten die folgenden Identitäten:
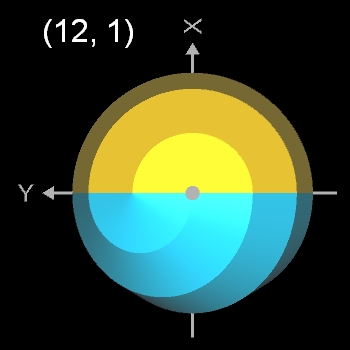
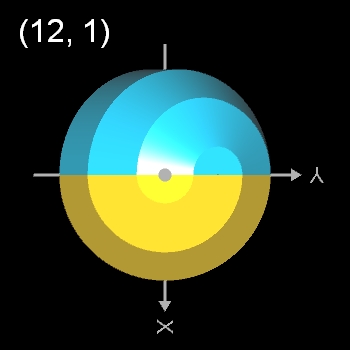
- (12, 1)-Dodecasphericon ≡ (12, 7)-Dodecasphericon
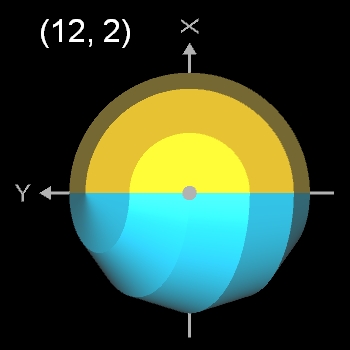
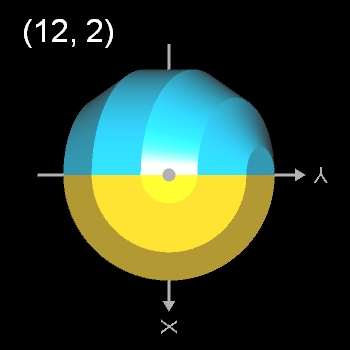
- (12, 2)-Dodecasphericon ≡ (12, 8)-Dodecasphericon
- (12, 3)-Dodecasphericon ≡ (12, 9)-Dodecasphericon
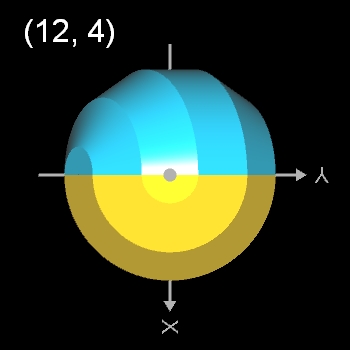
- (12, 4)-Dodecasphericon ≡ (12,10)-Dodecasphericon
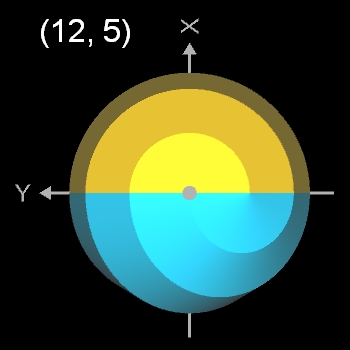
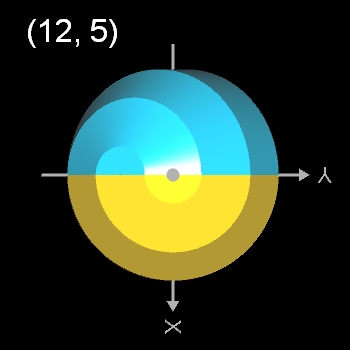
- (12, 5)-Dodecasphericon ≡ (12,11)-Dodecasphericon
Beim Dodecasphericon sind folgende Paare chiral (s. auch Galerie bei der entsprechenden Variante):
- (12, 1)- und (12, 5)-Dodecasphericon
- (12, 2)- und (12, 4)-Dodecasphericon.
Gerades Dodecasphericon
Beim geraden Dodecasphericon verläuft die Rotationsachse durch zwei gegenüberliegende Ecken
(s. folgende Grafik). Den Zusammenhang zwischen den k Drehungen einer Hälfte des Rotationskörpers um Winkelinkremente von 1 / 6
π zeigt die folgende Tabelle.
|
Gerades Dodecasphericon p = 12 |
|||||||
| k: |
0 6 |
1 7 |
2 8 |
3 9 |
4 10 |
5 11 |
|
| Flächen | 6 | 1 | 2 | 3 | 2 | 1 | |
| Kanten | 5 | 2 | 3 | 4 | 3 | 2 | |
Hinweis: Bei der Darstellung der geraden (12,k)-Dodecasphericons habe ich im Gegensatz zu den anderen Polysphericons auf meiner Seite auf die Animation "Halbieren des Rotationskörpers mit anschließenden k Drehungen" verzichtet. Stattdessen wird direkt das "fertige" (12,k)-Dodecasphericon mit unterschiedlich eingefärbten Seiten dargestellt und rotiert.
Die folgende Galerie zeigt die chiralen Paare des geraden Dodecasphericons.
Duales Dodecasphericon
Beim dualen Dodecasphericon verläuft die Rotationsachse durch die Mitten zweier gegenüberliegender Kanten (s. folgende Grafik). Die folgende Tabelle zeigt den Zusammenhang zwischen k Drehungen einer Hälfte des Rotationskörpers um Winkelinkremente von 1 / 6 π.
|
Duales Dodecasphericon p = 12 |
|||||||
| k: |
0 6 |
1 7 |
2 8 |
3 9 |
4 10 |
5 11 |
|
| Flächen | 7 | 2 | 3 | 4 | 3 | 2 | |
| Kanten | 6 | 1 | 2 | 3 | 2 | 1 | |
Hinweis: Auch bei der Darstellung der dualen (12,k)-Dodecasphericons wurde ohne vorherige Animation direkt das "fertige" (12,k)-Dodecasphericon mit unterschiedlich eingefärbten Seiten dargestellt und rotiert.
Die chiralen Paare des dualen Dodecasphericons sind in der folgenden Galerie dargestellt.