Hexasphericon (p=6)
Durch die Rotation eines regelmäßigen Sechsecks (Hexagon) um eine Achse in der Ebene des Sechsecks entsteht der Grundkörper für das Hexasphericon. Da p = 6 geradzahlig ist, gibt es die zwei Varianten gerades Hexasphericon und duales Hexasphericon. Bei beiden Varianten existieren auf Grund der Symmetrie außer dem Grundkörper (k = 0) jeweils nur zwei verschiedene Exemplare. Für beide Varianten gelten folgende Identitäten:
- (6, 1)-Hexasphericon ≡ (6, 4)-Hexasphericon
- (6, 2)-Hexasphericon ≡ (6, 5)-Hexasphericon
Außerdem sind die Paare (6, 1)- / (6, 2)-Hexasphericon und somit auch (6, 4)- / (6, 5)-Hexasphericon chiral.
Sehr ansprechende, aus Aluminium gefertigte Hexasphericons findet man bei [1], [2]. Bei der gelungenen Konstruktion enthalten die Hälften im Innern Magnete sowie eine gemeinsame Achse. So lassen sich beide Hälften leicht verdehen, halten aber dennoch perfekt zusammen. Auf der Seite gibt es auch ein Video, das die Rolleigenschaften des Hexasphericons verdeutlicht sowie andere "Objekte mit mathematischem Hintergrund".
Gerades Hexasphericon
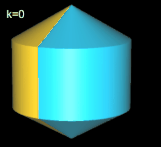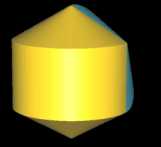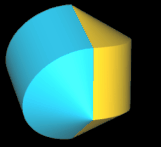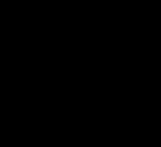
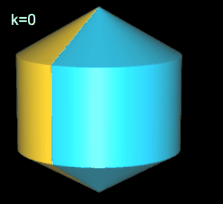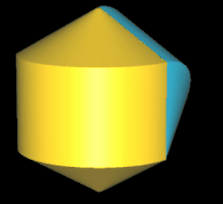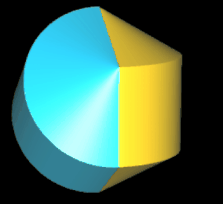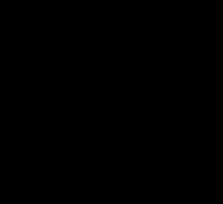
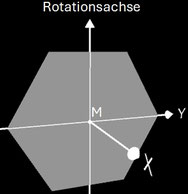
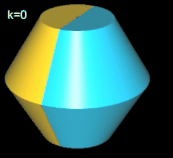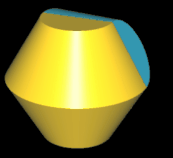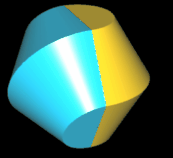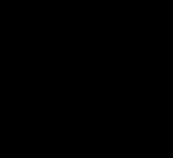
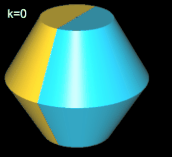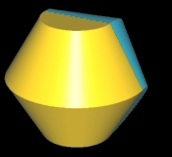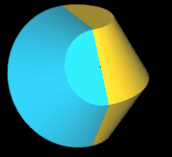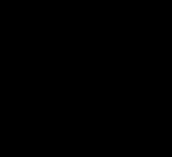
Beim geraden Hexasphericon verläuft die Rotationsachse durch zwei gegenüberliegende Ecken. Den Zusammenhang zwischen den k Drehungen einer Hälfte des Rotationskörpers um Winkelinkremente
von
1 / 3 π
zeigt die folgende Tabelle.
|
Gerades Hexasphericon p = 6 |
||||
| k: |
0 3 |
1 4 |
2 5 |
|
| Flächen | 3 | 1 | 1 | |
| Kanten | 2 | 2 | 2 | |
Hinweis: Um die Entstehung des Hexasphericons besser beobachten / nachvollziehen zu können, sind in den folgenden Animationen die beiden Hälften des Rotationskörpers unterschiedlich eingefärbt - vor und auch nach der Drehung - wenngleich die erzeugten Hexasphericons jeweils genau eine Fläche besitzen.
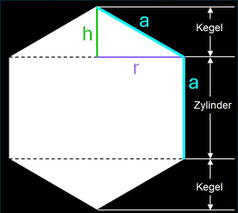
Für die Berechnung des Volumens und der Oberfläche des geraden Hexasphericons entnimmt man die erforderlichen Maße aus dem zu Grunde liegenden regelmäßigen Sechseck (s. Grafik rechts). Der Grundkörper vor erfolgten Drehungen besteht aus einem Zylinder mit oben und unten angesetzten komngruenten Kegeln.
Duales Hexasphericon
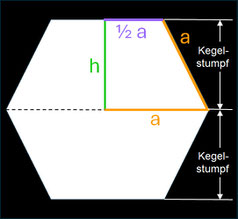
Beim dualen Hexasphericon verläuft die Rotationsachse durch die Mitten zweier gegenüberliegender Kanten. Die folgende Tabelle zeigt den Zusammenhang zwischen k Drehungen einer Hälfte des Rotationskörpers um Winkelinkremente von 1 / 3 π.
|
Duales Hexasphericon p = 6 |
||||
| k: |
0 3 |
1 4 |
2 5 |
|
| Flächen | 4 | 2 | 2 | |
| Kanten | 3 | 1 | 1 | |
Hinweis: Um die Entstehung des Hexasphericons besser beobachten / nachvollziehen zu können, sind in der folgenden Animation die beiden Hälften des Rotationskörpers unterschiedlich eingefärbt. Nach der Drehung wurden die beim erzeugten Hexasphericon entstandenen Flächen (jeweils 2) neu eingefärbt.
Beim dualen Hexasphericon besteht der Grundkörper vor erfolgten Drehungen aus zwei kongruenten Kegelstümpfen. Für die Berechnung des Volumens und der Oberfläche entnimmt man die erforderlichen Maße aus dem zu Grunde liegenden regelmäßigen Sechseck (s. Grafik rechts).
