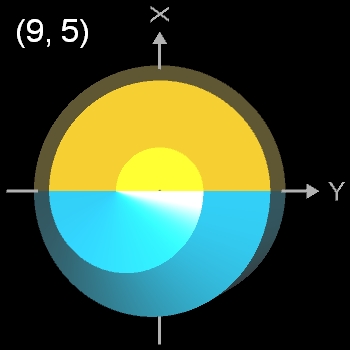
Nonasphericon (p=9)
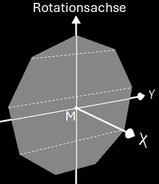
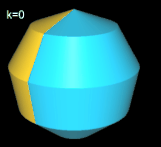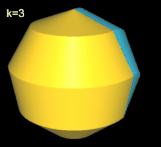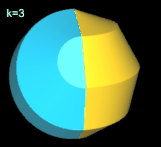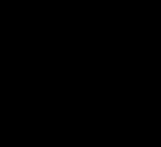
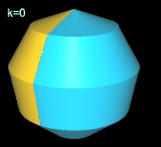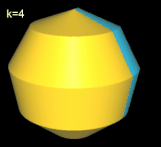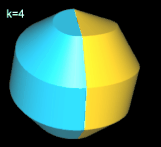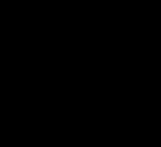
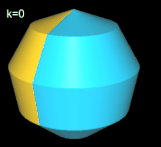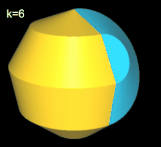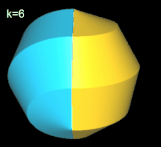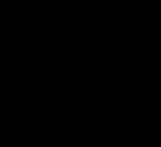
Basis für ein Nonasphericon ist das regelmäßige Nonagon (Neuneck), das um eine Höhenachse rotiert
(s. folgende Grafik). Durch die Drehung einer Hälfte des Rotationskörpers um einen Winkel von k∙2π / 9 mit k = 1, .., 8 entstehen die acht möglichen unterschiedlichen Nonasphericons.
Da p = 9 = 3² und 3 prim ist, haben die (p, k)-Nonasphericons mit k = 3, 6 mehr als eine Fläche (s. auch Polysphericons Grundlagen), während sie für alle anderen Werte von k genau eine Fläche aufweisen.
|
Nonasphericon |
||||||||||
| k: |
0 9 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Flächen | 5 | 1 | 1 | 2 | 1 | 1 | 2 | 1 | 1 | |
| Kanten | 4 | 1 | 1 | 2 | 1 | 1 | 2 | 1 |
1 |
|
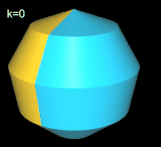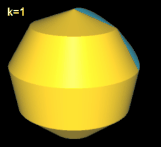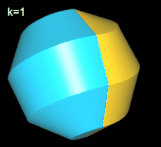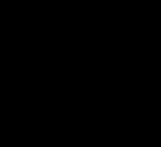
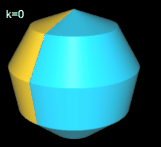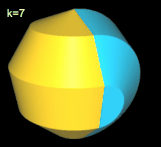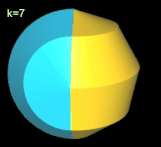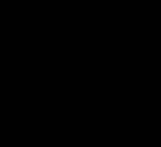
Hinweis: Um die Entstehung des Nonasphericons besser beobachten / nachvollziehen zu können, sind in den folgenden Animationen die beiden Hälften des Rotationskörpers unterschiedlich eingefärbt - vor und auch nach der Drehung - wenngleich die meisten erzeugten Heptasphericons genau eine Fläche besitzen.
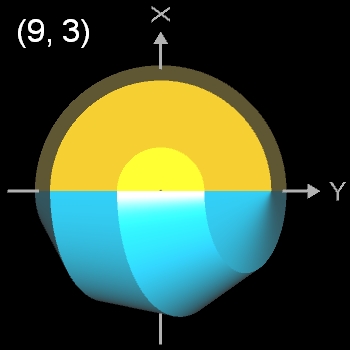
Für k = 3, 6 besitzt das Nonasphericon 2 Flächen, die nach der Drehung entsprechend neu gefärbt wurden:
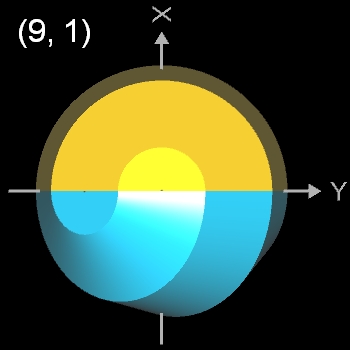
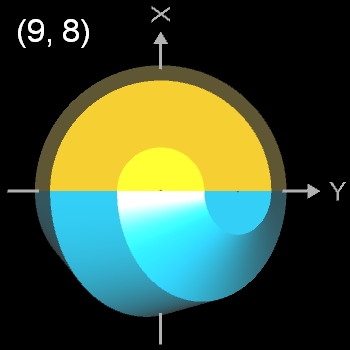
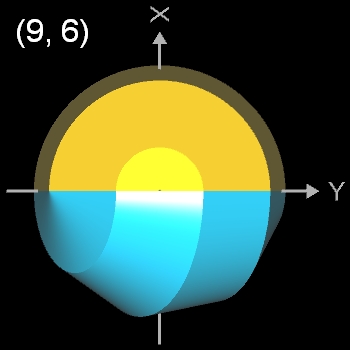
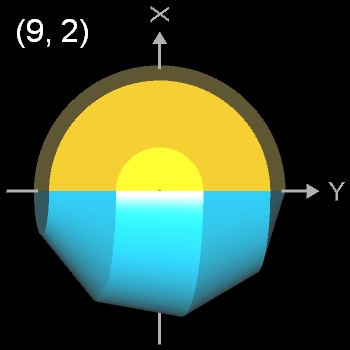
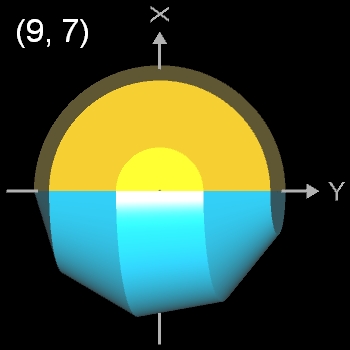
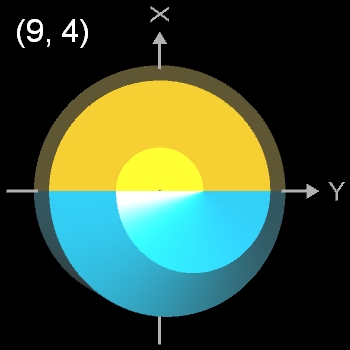
Beim Nonasphericon sind folgende Paare chiral (s. auch folgende Galerie):
- (9, 1)- und (9, 8)-Nonasphericon
- (9, 2)- und (9, 7)-Nonasphericon
- (9, 3)- und (9, 6)-Nonasphericon
- (9, 4)- und (9, 5)-Nonasphericon.