Octasphericon (p=8)

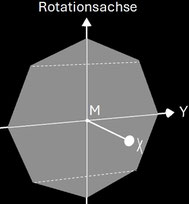
Der Grundkörper für das Octasphericon entsteht durch die Rotation eines regelmäßigen Sechsecks (Octagon) um eine Achse in der Ebene des Sechsecks. Es gibt die zwei Varianten gerades Octasphericon und duales Octasphericon, da p = 6 geradzahlig ist. Bei beiden Varianten existieren auf Grund der Symmetrie außer dem Grundkörper (k = 0) jeweils nur drei verschiedene Exemplare. Für beide Varianten gelten folgende Identitäten:

• (8, 1)-Octasphericon  ≡  (8, 5)-Octasphericon
• (8, 2)-Octasphericon  ≡  (8, 6)-Octasphericon
• (8, 3)-Octasphericon  ≡  (8, 7)-Octasphericon

Außerdem sind für beide Varianten die Paare (8, 1)- / (8, 3)-Octasphericon und (8, 5)- / (8, 7)-Octasphericon chiral.

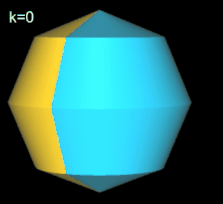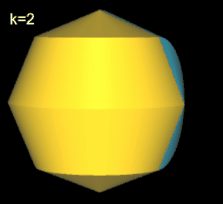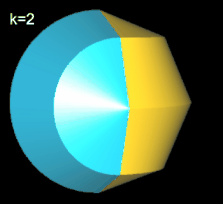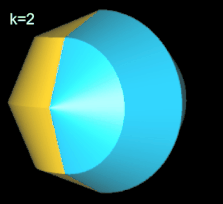
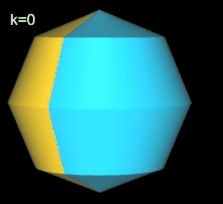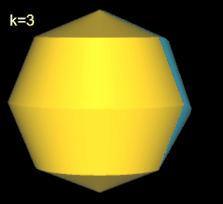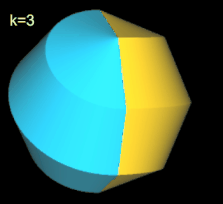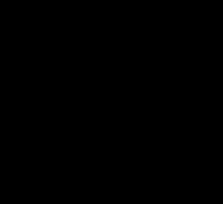
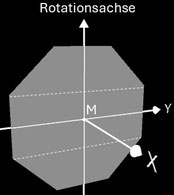
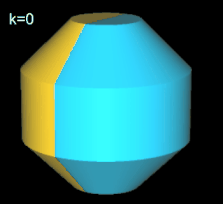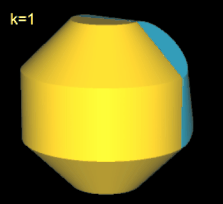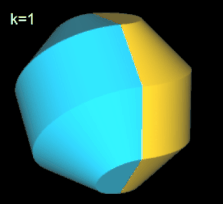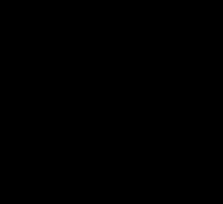
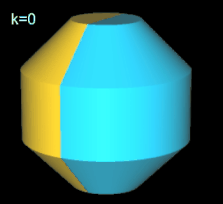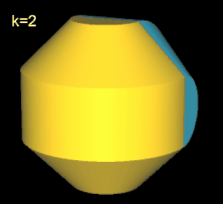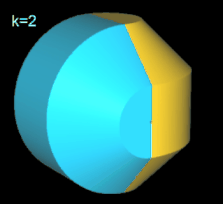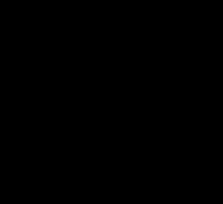
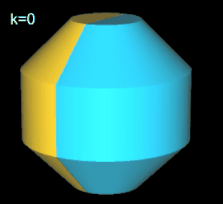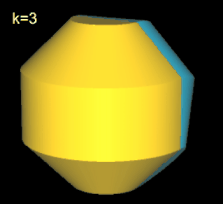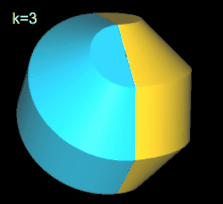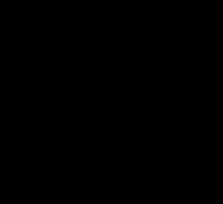
Beim geraden Octasphericon verläuft die Rotationsachse durch zwei gegenüberliegende Ecken. Den Zusammenhang zwischen den k Drehungen einer Hälfte des Rotationskörpers um Winkelinkremente von
1 / 4 π zeigt die folgende Tabelle.

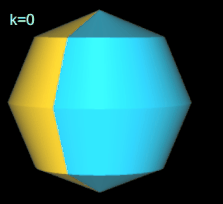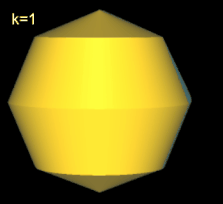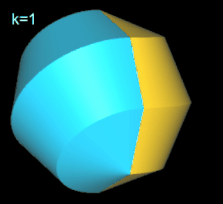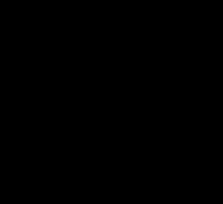
Hinweis: Um die Entstehung des Hexasphericons besser beobachten / nachvollziehen zu können, sind in den folgenden Animationen die beiden Hälften des Rotationskörpers unterschiedlich eingefärbt - vor und auch nach der Drehung.

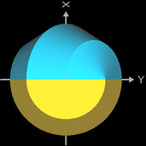
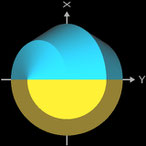
Für k = 2, 6 besitzt das Octasphericon 2 Flächen, die nach der Drehung entsprechend neu gefärbt wurden (s. nächste Galerie, linke Grafik). Weiterhin sind das gerade (8, 1)- und (8, 3)-Octasphericon und somit das gerade (8, 5)- und (8, 7)-Octasphericon chiral (s. dazu die mittlere und rechte Grafik in folgender Galerie).

Beim dualen Octasphericon verläuft die Rotationsachse durch die Mitten zweier gegenüberliegender Kanten. Die folgende Tabelle zeigt den Zusammenhang zwischen k Drehungen einer Hälfte des Rotationskörpers um Winkelinkremente von 1 / 4 π.

Hinweis: Um die Entstehung des Octasphericons besser beobachten / nachvollziehen zu können, sind in der folgenden Animation die beiden Hälften des Rotationskörpers unterschiedlich eingefärbt. Nach der Drehung wurden die beim erzeugten Octasphericon entstandenen Flächen neu eingefärbt.