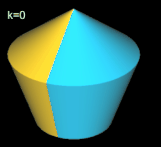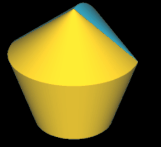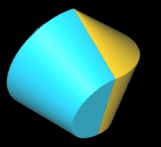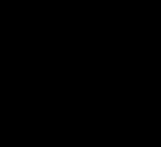
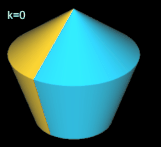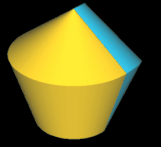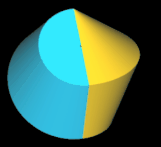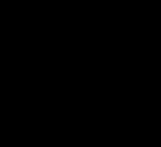
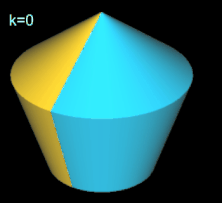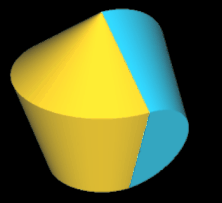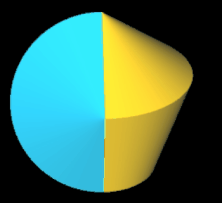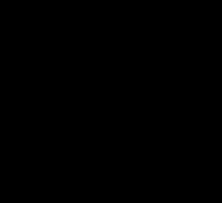
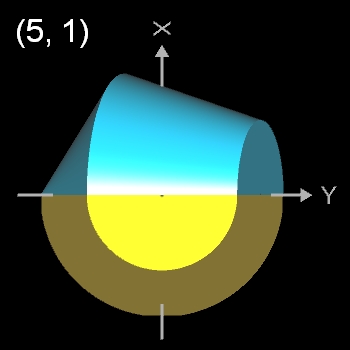
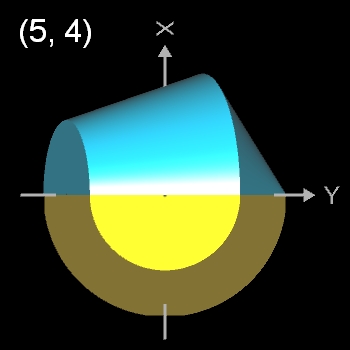
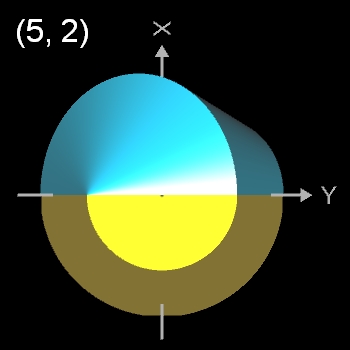
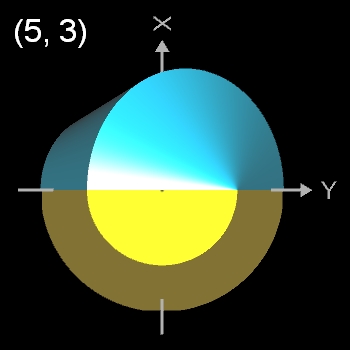
Pentasphericon (p=5)
Das Pentasphericon basiert auf einem regelmäßigen Pentagon (Fünfeck). Es gibt vier unterschiediche Pentasphericons, die durch die Drehung einer Hälfte des Rotationskörpers um einen Winkel von k∙2π/5 mit k = 1, .., 4 entstehen und die jeweils exakt eine Fläche und eine Kante aufweisen:
|
Pentasphericon p = 5 |
||||||
| k: |
0 |
1 | 2 | 3 | 4 | |
| Flächen | 3 | 1 | 1 | 1 | 1 | |
| Kanten | 2 | 1 | 1 | 1 | 1 | |
Hinweis: Um die Entstehung des Pentasphericons besser beobachten / nachvollziehen zu können, sind in den folgenden Animationen die beiden Hälften des Rotationskörpers unterschiedlich eingefärbt - vor und auch nach der Drehung - wenngleich die erzeugten Pentasphericons jeweils genau eine Fläche besitzen.
Beim Pentasphericon sind folgende Paare chiral (s. auch folgende Galerie):
- (5, 1)- und (5, 4)-Pentasphericon
- (5, 2)- und (5, 3)-Pentasphericon.
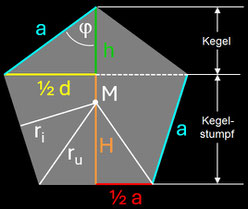
Für die Berechnung des Volumens und der Oberfläche des Pentasphericons entnimmt man die erforderlichen Maße aus dem zu Grunde liegenden regelmäßigen Fünfeck mit Seitenlänge a.
Der Grundkörper vor erfolgten Drehungen besteht aus einem Kegelstumpf mit oben angesetztem Kegel.
Die Oberfläche O des Pentasphericons besteht aus den Mantelfächen von Kegel und Kegelstumpf sowie einer Kreisfläche G mit Durchmesser a.
