Trisphericon (p=3)
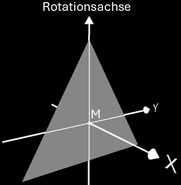
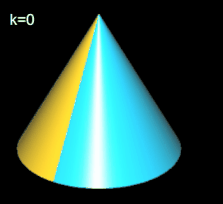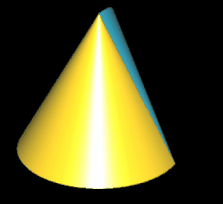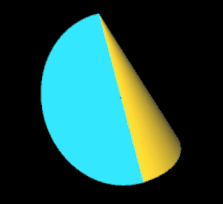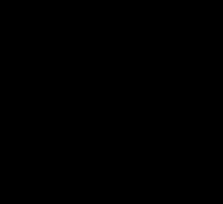
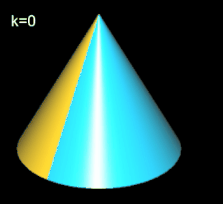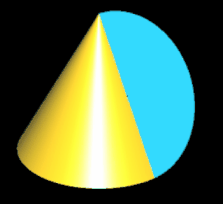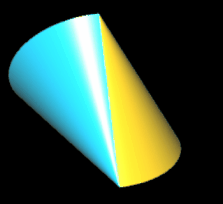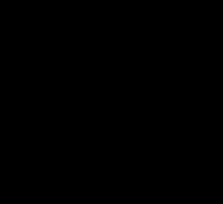
Das Trisphericon ist das einfachste Polysphericon. Es entsteht durch die Rotation eines gleichseitigen Dreiecks mit Seitenlänge a um eine Höhenachse (s. folgende Grafik) und anschließende Drehung einer Hälfte des durch die Rotation entstandenen Kegel um Winkelinkremente von 2 / 3 π. Während der Kegel zwei Flächen (Mantelfläche und Boden) sowie eine Kante besitzt, haben das (3, 1)- und das (3, 2)-Trisphericon jeweils genau eine Fläche und eine Kante und sind darüber hinaus chiral.
|
Trisphericon p = 3 |
||||
| k: |
0 |
1 | 2 | |
| Flächen | 2 | 1 | 1 | |
| Kanten | 1 | 1 | 1 | |
Hinweis: Um die Entstehung des Trisphericons besser beobachten / nachvollziehen zu können, sind in den folgenden Animationen die beiden Hälften des Rotationskörpers unterschiedlich eingefärbt - vor und auch nach der Drehung - wenngleich beide erzeugten Trisphericons jeweils genau eine Fläche besitzen.
Das Volumen des durch Rotation eines gleichseitigen Dreiecks mit Seitenlänge a erzeugten Trisphericons ist das Volumen eines Kegels:
Die Oberfläche des Trisphericons ergibt sich zu
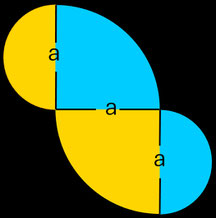
Die folgende Abbildung zeigt die abgewickelte Fläche des Trisphericons.
