sinc-Funktion
Die Nomenklatur für die analytische sinc-Funktion ist in der internationalen mathematischen Literatur nicht eindeutig festgelegt. Im Folgenden werden diese beiden Definitionen verwendet:
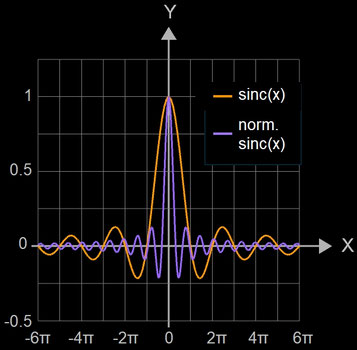
Die Funktion hat an der Stelle x = 0 eine hebbare Singularität und wird durch den Grenzwert sinc (0) = 1 stetig fortgesetzt. Die sinc-Funktion besitzt Nullstellen bei n∙π mit n ∈ ℤ \ {0}, während diese bei der normierten sinc-Funktion an den Stellen n ∈ ℤ \ {0} liegen.
Außer für den Extremwert bei x = 0 lassen sich die Positionen der Extremwerte der sinc-Funktion nicht durch algebraische Umformungen der Gleichungn d/dx sinc(x) = 0 ó (x∙cos(x) - sin(x)) / x² = 0 mit x ≠ 0 lösen, sondern müssen numerisch ermittelt werden. In [x] findet sich eine Näherungsformel für die Positionen xn mit n ≥ 1 der Extremwerte:
Für gerade n liegt ein relatives Maximum, für ungerade n ein relatives Minimum vor.
Die Näherungsformel ist recht gut, der größte absolute Fehler beträgt nur 0.15 %; mit zunehmendem x wird der absolute Fehler schnell kleiner:
| n | sin(x)-cos(x)=0 | Näherung | abs. Fehler |
| 5 | 17,22075527 | 17,2208851 | 0,00075% |
| 4 | 14,06619391 | 14,0664314 | 0,00169% |
| 3 | 10,90412166 | 10,9046286 | 0,00465% |
| 2 | 7,72525184 | 7,72665768 | 0,01820% |
| 1 | 4,49340946 | 4,50018239 | 0,15073% |
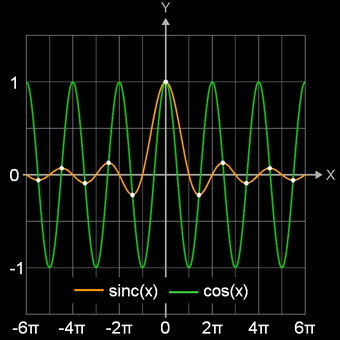
Die Extremwerte der sinc-Funktion (weiße Punkte in nebenstehender Grafik) sind identisch mit ihren Schnittpunkten mit der Cosinus-Funktion.
Für die komplexe sinc-Funktion f (z) = sinc (z) siehe unter 3D Visualisierung komplexwertiger Funktionen. Weitere Eigenschaften sowie Anwendungen der sinc-Funktion findet man bei [1].