Fresnel-Integral

Die Fresnel-Integrale S(x) und C(x) sind zwei uneigentliche Integrale:
Sie wurden nach Augustin-Jean Fresnel
(1788 – 1822) benannt und spielen eine Rolle bei Beugungserscheinungen in der Optik, in der Quantenmechanik und als Klothoiden bei der Trassierung
im Straßen- und Schienenbau und können nicht durch elementare Funktionen ausgedrückt werden.

Mit S(u) und C(u) lässt sich eine Klothoide herleiten. Hierzu werden S(u) über C(u) mit u als dritte räumliche Koordinate aufgetragen (s. Animation rechts).
Die entstehende Raumkurve ist eine 3D Cornu-Spirale im S(u)-C(u)-u-Koordinatensystem.
Die Parallelprojektion dieser Raumkurve in die
S(u)-u-Ebene und in die C(u)-u-Ebene ergibt die Funktionsgraphen für
S(u) und C(u).
Die Parallelprojektion der Raumkurve in die S(u)-C(u)-Ebene ergibt die Klothoide (weiß). Für negative Werte von u wird die Klothoide im dritten Quadranten fortgesetzt (gepunktet).
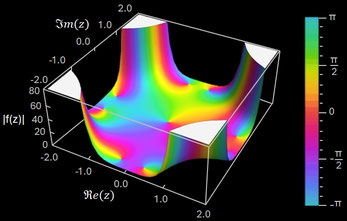
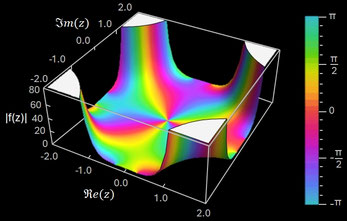
Die folgenden Abbildungen zeigen Betrag und Phase der komplexen Fresnel-Integrale C(z) und S(z) im Bereich -2-2i bis 2+2i.